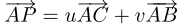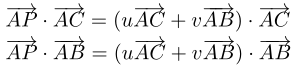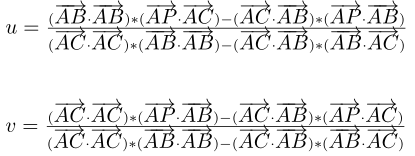数学基础
向量点乘(Dot Product)
点乘比较简单,是相应元素的乘积的和:
V1( x1, y1)+ V2(x2, y2) = x1*x2 + y1*y2
注意结果不是一个向量,而是一个标量(Scalar)。点乘有什么用呢,我们有:
= |A||B|Cos(θ)
θ是向量A和向量B见的夹角。这里|A|我们称为向量A的模(norm),也就是A的长度, 在二维空间中就是|A| = sqrt()。这样我们就和容易计算两条线的夹角:
Cos(θ) = / (|A||B|)
这可以告诉我们如果点乘的结果,简称点积,为0的话就表示这两个向量垂直。当两向量平行时,点积有最大值.
另外,点乘运算不仅限于2维空间,他可以推广到任意维空间.
叉乘(cross product)
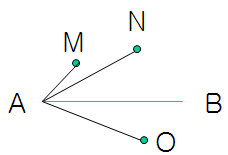
相对于点乘,叉乘可能更有用吧。2维空间中的叉乘是:
V1(x1, y1) X V2(x2, y2) = x1y2 -y1x2
看起来像个标量,事实上叉乘的结果是个向量,方向在z轴上。上述结果是它的模。在二维空间里,让我们暂时忽略它的方向,将结果看成一个向量,那么这个结果类似于上述的点积,我们有:
A x B = |A||B|Sin(θ)
然而角度 θ和上面点乘的角度有一点点不同,他是有正负的,是指从A到B的角度。
另外还有一个有用的特征那就是叉积的绝对值就是A和B为两边说形成的平行四边形的面积。也就是AB所包围三角形面积的两倍。这个还是很显然的啦。在计算面积时,我们要经常用到叉积。
一次牛客的比赛中遇到了这个题,当时是用下面的方法一来实现的,之后看了些博客,发现还有好几种更好的方法,当时实现起来代码还显得特别不好看2333,太菜了。

判断点在三角形内
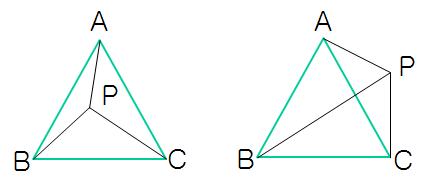
面积法
利用面积,如图中,求三角形面积的方法就可以用上面提到的利用叉积就行了,注意记得加上绝对值,因为叉积可能为负。还有种简单的方法是利用内角和为但效率低下,就不管了。
同侧法
首先看一下这个问题,如何判断某两个点在某条直线的同一侧

根据向量的叉乘以及右手螺旋定则,AB^AM (^表示叉乘,这里向量省略了字母上面的箭头符号)的方向为向外指出屏幕,AB^AN也是向外指出屏幕,但AB^AO的方向是向内指向屏幕,因此M,N在直线AB的同侧,M ,O在直线AB的两侧。实际计算时,只需要考虑叉积的数值正负假设以上各点坐标为A(0,0), B(4,0), M(1,2), N(3,4), O(3,-4), 则:
AB^AM = (4,0)^(1,2) = 4*2 - 0*1 = 8
AB^AN = (4,0)^(3,4) = 4*4 – 0*3 = 16
AB^AO = (4,0)^(3,-4) = 4*-4 – 0*3 = –16
由上面的数值可知,可以根据数值的正负判断叉乘后向量的方向。即,如果叉积AB^AM 和 AB^AN的结果同号,那么M,N两点就在直线的同侧,否则不在同一侧。特殊地,如果点M在直线AB上,则AB^AM的值为0。(如果是在三维坐标系中,求出的叉积是一个向量,可以根据两个向量的点积结果正负来判断两个向量的是否指向同一侧)。
以上的问题解决了,就很容易的用来判断某个点是否在三角形内,如果P在三角形ABC内部,则满足以下三个条件:P,A在BC的同侧、P,B在AC的同侧、PC在AB的同侧。某一个不满足则表示P不在三角形内部。
一个不知道怎么命名的方法
该方法也用到了向量。对于三角形ABC和一点P,可以有如下的向量表示:

p点在三角形内部的充分必要条件是:1 >= u >= 0, 1 >= v >= 0, u+v <= 1。
已知A,B,C,P四个点的坐标,可以求出u,v,把上面的式子分别点乘向量AC和向量AB

解方程得到:

解出u,v后只需要看他们是否满足“1 >= u >= 0, 1 >= v >= 0, u+v <= 1”,如满足,则,p 在三角形内。
(u = 0时,p在AB上, v = 0时,p在AC上,两者均为0时,p和A重合)
又一个不知道怎么命名的算法
该算法和算法2类似,可以看作是对算法2的简化,也是用到向量的叉乘。假设三角形的三个点按照顺时针(或者逆时针)顺序是A,B,C。对于某一点P,求出三个向量PA,PB,PC, 然后计算以下三个叉乘(^表示叉乘符号):
t1 = PA^PB,
t2 = PB^PC,
t3 = PC^PA,
如果t1,t2,t3同号(同正或同负),那么P在三角形内部,否则在外部。
经过测试,算法4最快,算法3次之,接着算法2,算法1最慢。直观的从计算量上来看,也是算法4的计算量最少。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
| #include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<iostream>
#include<algorithm>
#include<stack>
#include<queue>
#include<vector>
#include<list>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
class Vector2d
{
public:
double x_;
double y_;
public:
Vector2d(double x, double y):x_(x), y_(y){}
Vector2d():x_(0), y_(0){}
double CrossProduct(const Vector2d vec)
{
return x_*vec.y_ - y_*vec.x_;
}
double DotProduct(const Vector2d vec)
{
return x_ * vec.x_ + y_ * vec.y_;
}
Vector2d Minus(const Vector2d vec) const
{
return Vector2d(x_ - vec.x_, y_ - vec.y_);
}
static bool IsPointAtSameSideOfLine(const Vector2d &pointM, const Vector2d &pointN,
const Vector2d &pointA, const Vector2d &pointB)
{
Vector2d AB = pointB.Minus(pointA);
Vector2d AM = pointM.Minus(pointA);
Vector2d AN = pointN.Minus(pointA);
return AB.CrossProduct(AM) * AB.CrossProduct(AN) >= 0;
}
};
class Triangle
{
public:
Vector2d pointA_, pointB_, pointC_;
public:
Triangle(Vector2d point1, Vector2d point2, Vector2d point3)
:pointA_(point1), pointB_(point2), pointC_(point3){}
Triangle():pointA_(), pointB_(), pointC_(){};
double ComputeTriangleArea()
{
Vector2d AB = pointB_.Minus(pointA_);
Vector2d BC = pointC_.Minus(pointB_);
return fabs(AB.CrossProduct(BC) / 2.0);
}
bool IsPointInTriangle1(const Vector2d pointP)
{
double area_ABC = ComputeTriangleArea();
double area_PAB = Triangle(pointP, pointA_, pointB_).ComputeTriangleArea();
double area_PAC = Triangle(pointP, pointA_, pointC_).ComputeTriangleArea();
double area_PBC = Triangle(pointP, pointB_, pointC_).ComputeTriangleArea();
if(fabs(area_PAB + area_PBC + area_PAC - area_ABC) < 0.000001)
return true;
else return false;
}
bool IsPointInTriangle2(const Vector2d pointP)
{
return Vector2d::IsPointAtSameSideOfLine(pointP, pointA_, pointB_, pointC_) &&
Vector2d::IsPointAtSameSideOfLine(pointP, pointB_, pointA_, pointC_) &&
Vector2d::IsPointAtSameSideOfLine(pointP, pointC_, pointA_, pointB_);
}
bool IsPointInTriangle3(const Vector2d pointP)
{
Vector2d AB = pointB_.Minus(pointA_);
Vector2d AC = pointC_.Minus(pointA_);
Vector2d AP = pointP.Minus(pointA_);
double dot_ac_ac = AC.DotProduct(AC);
double dot_ac_ab = AC.DotProduct(AB);
double dot_ac_ap = AC.DotProduct(AP);
double dot_ab_ab = AB.DotProduct(AB);
double dot_ab_ap = AB.DotProduct(AP);
double tmp = 1.0 / (dot_ac_ac * dot_ab_ab - dot_ac_ab * dot_ac_ab);
double u = (dot_ab_ab * dot_ac_ap - dot_ac_ab * dot_ab_ap) * tmp;
if(u < 0 || u > 1)
return false;
double v = (dot_ac_ac * dot_ab_ap - dot_ac_ab * dot_ac_ap) * tmp;
if(v < 0 || v > 1)
return false;
return u + v <= 1;
}
bool IsPointInTriangle4(const Vector2d pointP)
{
Vector2d PA = pointA_.Minus(pointP);
Vector2d PB = pointB_.Minus(pointP);
Vector2d PC = pointC_.Minus(pointP);
double t1 = PA.CrossProduct(PB);
double t2 = PB.CrossProduct(PC);
double t3 = PC.CrossProduct(PA);
return t1*t2 >= 0 && t1*t3 >= 0 &&t2*t3>=0;
}
};
int main(){
Triangle a;
while(scanf("%lf%lf%lf%lf%lf%lf",&a.pointA_.x_,&a.pointA_.y_,&a.pointB_.x_,&a.pointB_.y_,&a.pointC_.x_,&a.pointC_.y_)!=EOF){
Vector2d p;
scanf("%lf%lf",&p.x_,&p.y_);
if(a.IsPointInTriangle1(p)) printf("YES\n");
else printf("NO\n");
}
return 0;
}
|